品質管理はデータに始まり、データで終わります。

1. 多元配置分散分析（ｎ＝１）とは

（解説）
　1.多元配置分散分析（ｎ＝１）について、説明して
　　行きます。
　2.多元配置分散分析（ｎ＝１）は、以下の場合です。
　　・要因　　：　３つ以上
　　・繰り返し：　ｎ＝１
　3.具体例は、次の通りです。
　　・要因１　：　温度A₁,A₂
　　・要因２　：　圧力B₁,B₂,B₃
　　・要因３　：　圧力C₁,C₂
　　・繰り返し：　ｎ＝１

4.要因が３つ以上で、繰り返し無し（ｎ＝１）の実験に用います。

---

2. データ例

（解説）
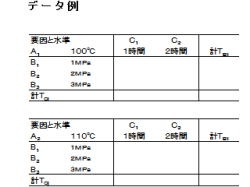
　1.データ例について、説明して行きます。
　2.左図の表を作成します。三元の表は見辛いので、
　　二元の表を２つ作ります。
　3.左の列には、要因と水準、計Ｔ_Ｃｊを記載します。
　・要因と水準、計Ｔ_Ｃｊ
　・Ａ_１　１００℃
　・Ｂ_１　１ＭＰａ　〜　Ｂ_３　３ＭＰａ
　・計Ｔ_Ｃｊ

4.上の行には、要因と水準を記載します。
　・要因と水準
　・Ｃ_１　１時間　〜　Ｃ_２　２時間
5.右の列には、計Ｔ_Ｂｉを記載します。
　・計Ｔ_Ｂｉ
6.同様な表を下にも作ります。Ａ_２　１１０℃の表です。

---

3. 平方和の分解

（解説）
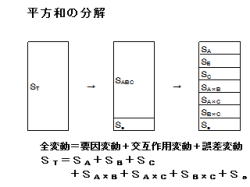
　1.平方和の分解について、説明して行きます。
　2.全変動Ｓ_Ｔは、要因変動Ｓ_Ａ、Ｓ_Ｂ、Ｓ_Ｃ、
　　交互作用変動Ｓ_Ａ×Ｂ、Ｓ_Ａ×Ｃ、Ｓ_Ｂ×Ｃ、
　　誤差変動Ｓ_ｅに分解できます。
　　・全変動＝要因変動＋交互作用変動＋誤差変動
　　・Ｓ_Ｔ＝Ｓ_ＡＢC＋Ｓ_ｅ＝Ｓ_Ａ＋Ｓ_Ｂ＋Ｓ_Ｃ
　　　　　　＋Ｓ_Ａ×Ｂ＋Ｓ_Ａ×Ｃ＋Ｓ_Ｂ×Ｃ＋Ｓ_ｅ
　3.上記の平方和の分解を理解すれば、分散分析の理解
　　が容易となります。

---

4. 実験データの入力

（解説）
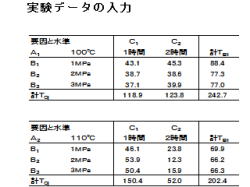
　1.実験データの入力について、説明して行きます。
　2.左図の表に実験データを入力します。
　3.真ん中の欄に、実験データを入力します。
　　・データｘ_ｉｊｋ
　4.右の列では、計Ｔ_Ｂｉを計算します。
　　・計Ｔ_Ｂｉ
　5.下の行では、計Ｔ_Ｃｊを計算します。
　　・計Ｔ_Ｃｊ
　6.右下の欄では、総計を計算します。
　　・総計

7.下の表も同様に計算します。

---

5. 分散分析表の作成

（解説）
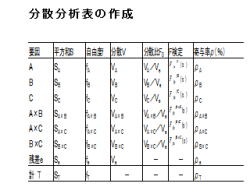
　1.分散分析表の作成について、説明して行きます。
　2.分散分析表は、下記の７つの項目を記載します。
　　・要因
　　・平方和Ｓ
　　・自由度ｆ
　　・分散Ｖ
　　・分散比Ｆ_０
　　・Ｆ検定
　　・寄与率ρ（％）

3.要因の列は、以下を記載します。
　・要因Ａ
　・要因Ｂ
　・要因Ｃ
　・交互作用Ａ×Ｂ
　・交互作用Ａ×Ｃ
　・交互作用Ｂ×Ｃ
　・残差e
　・計Ｔ

---

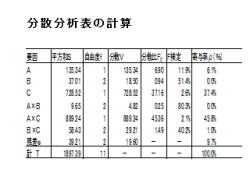
6. 分散分析表の計算

（解説）
　1.分散分析表の計算について、説明して行きます。
　2.下記の項目を計算します。
　　・平方和Ｓ
　　・自由度ｆ
　　・分散Ｖ
　　・分散比Ｆ_０
　　・Ｆ検定
　　・寄与率ρ（％）

3.Ｆ検定
　・要因Ａ
　　ｐ値は１１．９％となり、有意差は有りませんでした。
　　しかし、１２％の有意水準では有意となるので、要因Ａの水準を変化させると、特性値の平均値が
　　変わる可能性が有ります。
　・要因Ｂ
　　ｐ値は５１．４％となり、有意差は有りませんでした。
　　よって、要因Ｂは影響が無い事が判明しました。
　・要因Ｃ
　　ｐ値は２．６％となり、５％の有意水準で有意となりました。
　　よって、要因Ｃの水準を変化させると、特性値の平均値が変わる事が判明しました。
　・交互作用Ａ×Ｂ
　　ｐ値は８０．３％となり、有意差は有りませんでした。
　　よって、交互作用Ａ×Ｂは影響が無い事が判明しました。
　・交互作用Ａ×Ｃ
　　ｐ値は２．１％となり、５％の有意水準で有意となりました。
　　よって、交互作用Ａ×Ｃの水準を変化させると、特性値の平均値が変わる事が判明しました。
　・交互作用Ｂ×Ｃ
　　ｐ値は４０．２％となり、有意差は有りませんでした。
　　よって、交互作用Ｂ×Ｃは影響が無い事が判明しました。
4.寄与率ρ（％）
　・要因Ｃの寄与率は３７．４％、交互作用Ａ×Ｃの寄与率は４５．８％でした。
　・従って、全体のバラツキの８３．２％は、要因Ｃ及び交互作用Ａ×Ｃで説明できます。
　・要因Ｃ及び交互作用Ａ×Ｃで、八割方の制御が可能です。

---

7. 計算式の補足

（解説）
　1.計算式の補足ついて、説明して行きます。
　2.計算式は、下記の通りです。
　　・ＣＴ＝T^２／Ｎ＝
　　・Ｓ_Ｔ＝Σｘ_ｉｊｋ^２−ＣＴ＝
　　・Ｓ_Ａ＝Σ（Ｔ_Ａｉ^２／ｂｃ）−ＣＴ＝
　　・Ｓ_Ｂ＝Σ（Ｔ_Ｂｊ^２／ａｃ）−ＣＴ＝
　　・Ｓ_Ｃ＝Σ（Ｔ_Ｃｋ^２／ａｂ）−ＣＴ＝
　　・Ｓ_ＡＢ＝Σ（Ｔ_ＡｉＢｊ^２／ｃ）−ＣＴ＝
　　・Ｓ_ＡＣ＝Σ（Ｔ_ＡｉＣｋ^２／ｂ）−ＣＴ＝
　　・Ｓ_ＢＣ＝Σ（Ｔ_ＢｊＣｋ^２／ａ）−ＣＴ＝

　・Ｓ_Ａ×Ｂ＝Ｓ_ＡＢ−Ｓ_Ａ−Ｓ_Ｂ＝
　・Ｓ_Ａ×Ｃ＝Ｓ_ＡＣ−Ｓ_Ａ−Ｓ_Ｃ＝
　・Ｓ_Ｂ×Ｃ＝Ｓ_ＢＣ−Ｓ_Ｂ−Ｓ_Ｃ＝
　・Ｓ_ｅ＝Ｓ_Ｔ−Ｓ_Ａ−Ｓ_Ｂ−Ｓ_Ｃ−Ｓ_Ａ×Ｂ−Ｓ_Ａ×Ｃ＋Ｓ_Ｂ×Ｃ＝
　・ｆ_Ｔ＝ａｂｃ−１＝
　・ｆ_Ａ＝ａ−１＝
　・ｆ_Ｂ＝ｂ−１＝
　・ｆ_Ｃ＝ｃ−１＝
　・ｆ_ＡＢ＝ａｂ−１＝
　・ｆ_ＡＣ＝ａｃ−１＝
　・ｆ_ＢＣ＝ｂｃ−１＝
　・ｆ_Ａ×Ｂ＝ｆ_ＡＢ−ｆ_Ａ−ｆ_Ｂ＝
　・ｆ_Ａ×Ｃ＝ｆ_ＡＣ−ｆ_Ａ−ｆ_Ｃ＝
　・ｆ_Ｂ×Ｃ＝ｆ_ＢＣ−ｆ_Ｂ−ｆ_Ｃ＝
　・ｆ_ｅ＝ｆ_Ｔ−ｆ_Ａ−ｆ_Ｂ−ｆ_Ｃ−ｆ_Ａ×Ｂ−ｆ_Ａ×Ｃ−ｆ_Ｂ×Ｃ＝

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）