品質管理はデータに始まり、データで終わります。

1. 分散の加法性とは

（解説）
　1.分散の加法性について、説明して行きます。
　2.バラツキの指標として、分散が有ります。
　3.分散は加法性が成り立ち、足し算が可能です。
　4.部品１と部品２を組み合わせて製品を作る場合、
　　製品の分散は部品１の分散と部品２の分散の合計
　　となります。
　5.バラツキを計算するとき、加法性が成り立つと
　　計算が容易になります。

---

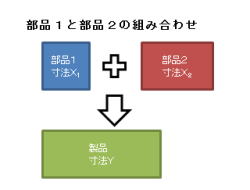
2. 部品１と部品２の組み合わせ

（解説）
　1.部品１と部品２の組み合わせについて、説明して
　　行きます。
　2.部品１と部品２を組み合わせて、製品を作ります。
　3.作り方は、左図の様に繋げる方法です。
　4.それぞれの寸法は、以下の通りです。
　　部品１：　寸法Ｘ_１
　　部品２：　寸法Ｘ_２
　　製品　：　寸法Ｙ
　5.寸法の関係は、次の様になります。
　　Ｙ＝Ｘ_１＋Ｘ_２

---

3. 平均値と分散

（解説）
　1.平均値と分散について、説明して行きます。
　2.平均値は加法性が成り立ち、下式となります。
　　Ｙ＝Ｘ_１＋Ｘ_２
　3.分散は加法性が成り立ち、下式となります。
　　σ_Ｙ^２＝σ_Ｘ１^２＋σ_Ｘ２^２
　4.ここで注意して欲しいのは、標準偏差は加法性が
　　成り立たない事です。
　　σ_Ｙ≠σ_Ｘ１＋σ_Ｘ２

---

4. 分散と標準偏差の関係

（解説）
　1.分散と標準偏差の関係について、説明して行き
　　ます。
　2.バラツキの指標として、下記の２つが有ります。
　　この２つの内、標準偏差の方が有名でしょうか。
　　分散　　：　σ_Ｙ^２
　　標準偏差：　σ_Ｙ
　3.分散と標準偏差は、次の様な関係が有ります。
　　σ_Ｙ＝ｓｑｒｔ（σ_Ｙ^２）

---

5. 標準偏差から計算する方法

（解説）
　1.標準偏差から計算する方法について、説明して
　　行きます。
　2.部品１の標準偏差と部品２の標準偏差が判明して
　　いる場合、製品の標準偏差が計算出来ます。
　3.部品の標準偏差を以下とします。
　　部品１：　σ_Ｘ１
　　部品２：　σ_Ｘ２
　4.この時、製品の標準偏差は、下記の通りです。
　　製品　：　σ_Ｙ＝ｓｑｒｔ（σ_Ｘ１^２＋σ_Ｘ２^２）

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）