品質管理はデータに始まり、データで終わります。

1. 正規分布

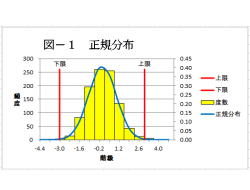
（解説）
　1.正規分布は、確率分布の中で最も有名です。
　2.製造工程からデータを取ると、正規分布に近く
　　なる事が多いです。
　3.統計的手法の中には、分布が正規分布である事を
　　前提にしているものが多いです。
　　（ｔ検定、Ｆ検定）
　4.工程能力指数Ｃｐ、Ｃｐｋの算出にも、正規分布
　　が用いられます。

---

2. 一様分布

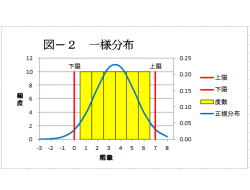
（解説）
　1.一様分布は、全ての階級の頻度が同じ分布です。
　2.例として、サイコロの出目が上げられます。
　3.サイコロの出目は、１〜６までの整数しか無い
　　ので、階級数は６となります。
　4.各出目の確率は、１／６≒０．１６となります。

---

3. 二項分布

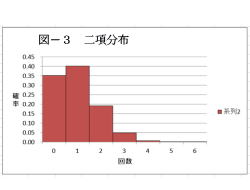
（解説）
　1.二項分布は、事象が起きる確率の分布です。
　2.例として、サイコロの出目が上げられます。
　3.各出目の確率は、１／６≒０．１６となります。
　4.試行回数が６回の場合は、１の目が出る回数の
　　確率は下記の様になります。
　　０回出る確率：　０．３５
　　１回出る確率：　０．４０
　　２回出る確率：　０．１９
　　３回出る確率：　０．０５
　　４回出る確率：　０．０１

---

4. ポアソン分布

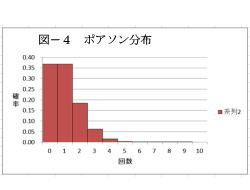
（解説）
　1.ポアソン分布は、単位当たり（時間、距離など）
　　に起きる回数の分布です。
　2.例として、電話が鳴る回数が上げられます。
　3.電話が鳴る回数が１回／時間の場合、１時間で
　　電話が鳴る回数の確率は下記の様になります。
　　０回鳴る確率：　０．３７
　　１回鳴る確率：　０．３７
　　２回鳴る確率：　０．１８
　　３回鳴る確率：　０．０６
　　４回鳴る確率：　０．０２

---

5. ｔ分布

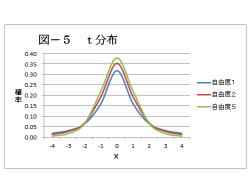
（解説）
　1.ｔ分布は、正規分布に似た分布です。
　2.自由度が大きくなると、正規分布に近づきます。
　3.サンプル数が少ない場合、母集団の平均値を
　　検定・推定するとき（ｔ検定）に使用されます。
　4.ｔ分布は、スチューデントのｔ分布とも言われて
　　います。
　5.これは１９０８年にウィリアム・ゴセットにより
　　発表されました。

---

6. F分布

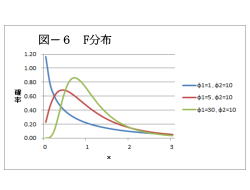
（解説）
　1.Ｆ分布は、母集団の分散を検定・推定するとき
　　（Ｆ検定）に使用されます。
　2.分散＝標準偏差＾２　の関係にあります。
　3.よって分散が等しい場合は、標準偏差も同じで
　　バラツキが等しいです。
　4.工程改善を行った場合のバラツキ改善度合いを
　　調べるのに使われます。

---

7. カイ２乗分布

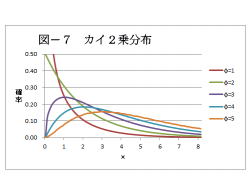
（解説）
　1.カイ２乗分布は、データが特定の比率で分布
　　しているかどうかを調べる（カイ２乗検定）
　　ときに使用されます。
　2.これは応用範囲が広く、データが正規分布か
　　どうかを調べる（正規性の検定）にも使えます。
　3.また母標準偏差の検定・推定にも用います。

---

8. ワイブル分布

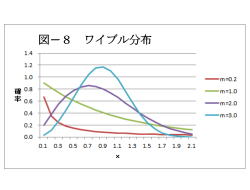
（解説）
　1.ワイブル分布は、引張試験などの最も弱い部分
　　が破壊する試験のモデルとして提案されました。
　2.また部品に対しての、熱劣化、摩耗劣化、経時
　　劣化、疲労劣化など故障現象にも応用できます。
　3.故障現象をワイブル分布で解析することにより、
　　初期故障、偶発故障、摩耗故障が分かります。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）