品質管理はデータに始まり、データで終わります。

1. 度数分布表とは

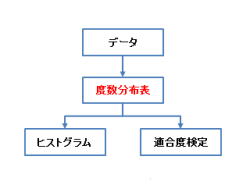
（解説）
　1.度数分布表について、説明して行きます。
　2.度数分布表は、ヒストグラムや適合度検定の元に
　　なる表です。
　3.統計的手法を活用するには、得られたデータを適切
　　に加工する事が必要です。
　4.データは数値の集まりに過ぎず、見ていても何の
　　意味が有るか分かりません。
　5.人間がデータの意味を理解するには、グラフや表に
　　変換する必要が有ります。

---

2. データを集める

（解説）
　1.データを集めるについて、説明して行きます。
　2.当たり前の事ですが、まずはデータを集める事から
　　始めます。
　3.データを集めたら、以後のデータ加工が容易な
　　エクセルに入力しましょう。
　4.入力する形式は、縦に並べる、横に並べる、表に
　　並べる等が有りますが、活用し易い形式を選び
　　ましょう。
　5.ファイルを保存する場合は、後で見て内容が分かり
　　易いファイル名にしましょう。日付も大事です。

---

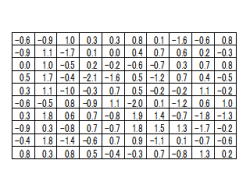
3. 最大値と最小値を見つける

（解説）
　1.最大値と最小値を見つけるについて、説明して
　　行きます。
　2.以降は、度数分布表を作る具体的な手順です。
　3.まず、データの最小値と最小値を見つけます。
　4.エクセルでは、下記の関数が使用できます。
　　・最大値：　=MAX(A1:A100)
　　・最小値：　=MIN(A1:A100)
　5.左記のデータでは、下記の様になります。
　　．最大値＝　１．９
　　．最小値＝−２．１

---

4. 仮の区間の数を決める

（解説）
　1.仮の区間の数を決めるについて、説明して行き
　　ます。
　2.次は、仮の区間の数を決めます。
　3.後に区間の数を修正する為、「仮の」と言いう言葉
　　を付けています。
　4.区間の数は、スタージェスの公式や平方根の選択で
　　決まるのが一般的です。
　5.本説明では、スタージェスの公式を使用して行き
　　ます。

6.スタージェスの公式は、下記の様になっています。
　・ｋ＝ｌｏｇ_２ｎ＋１
7.事例では、データ数ｎ＝１００なので、７．６４となります。
8.これを切り捨てて整数にします。結果は、７です。
9.エクセル関数では、下記の様になります。
　・=INT(LOG(100,2)+1)

---

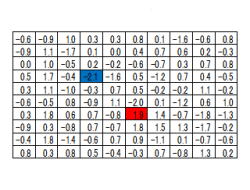
5. 測定単位を調べる

（解説）
　1.測定単位を調べるについて、説明して行きます。
　2.測定単位を調べるには、データの小数点以下の桁数
　　を調べます。
　3.全てのデータで、最も小数点以下の桁数が大きい
　　桁数を測定単位に使います。
　4.左表の場合は、１桁となりますので、測定短期は
　　０．１です。

---

6. 区間の幅を決める

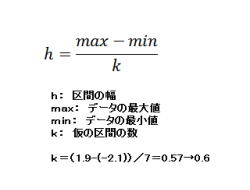
（解説）
　1.区間の幅を決めるについて、説明して行きます。
　2.そして、区間の幅を決めます。
　3.区間の幅は、データの最大値、データの最小値、
　　仮の区間の数より求めます。
　4.左記の事例では区間の幅ｈ＝０．５７となります。
　5.区間の幅が余りにも細かいと、度数分布表が分かり
　　難くなります。
　6.その為、区間の幅を測定単位の倍数になる様に加工
　　します。結果、区間の幅ｈ＝０．６です。

7.エクセル関数では、下記の様になります。
　・=MROUND(0.57,0.1)

---

7. 区間の数を修正する

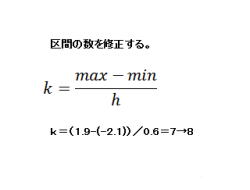
（解説）
　1.区間の数を修正するについて、説明して行きます。
　2.次は、区間の数を修正します。
　3.これは、区間の幅を測定単位の倍数にした為、
　　このままでは全データが区間の幅×区間の数の間に
　　入らなくなる恐れが有る為です。
　4.区間の数は、最大値、最小値、区間の幅より算出
　　します。
　5.その後、小数点第一位を切り上げます。
　6.最後に、仮の区間と数と修正後の区間の数が同じ
　　場合は、１を加えます。

7.エクセル関数では、下記の様になります。
　・=ROUNDUP((1.9-(-2.1))/0.6,0) (=kとする)
　・=IF(k=7,7+1,7)

---

8. 階級の下限、上限、中央を決める

（解説）
　1.階級の下限、上限、中央を決めるについて、説明
　　して行きます。
　2.そして、階級を決めます。
　3.階級を決めるには、階級の下限、階級の上限、階級
　　の中央を算出する必要があります。
　4.計算式は、下記の通りです。
　　・階級の下限＝最小値−測定単位／２
　　・階級の上限＝階級の下限＋区間の幅
　　・階級の中央＝（階級の上限＋階級の下限）／２

---

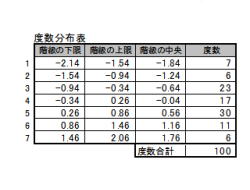
9. 度数分布表を作る

（解説）
　1.度数分布表を作るについて、説明して行きます。
　2.最後に度数分布表を作成します。
　3.左図の様な表を作り、それぞれの階級に該当する
　　データの個数を入力して行きます。
　4.このデータの個数の事を度数と呼びます。
　5.本事例では、データ数ｎ＝１００なので、度数合計
　　も１００になります。
　6.データ数ｎと度数合計が異なる場合は、何らかの
　　ミスを犯しているので、やり方を確認して下さい。

7.度数の分布を示している表なので、度数分布表と呼ばれています。
8.上記の度数分布表を見るだけでも、分布が二山になっている事が推測できます。
9.この度数分布表を元にして、ヒストグラムや適合度検定が出来る様になります。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）