品質管理はデータに始まり、データで終わります。

1. 和の分布とは

（解説）
　1.和の分布について、説明して行きます。
　2.和の分布は、２つ以上の独立変数を合計した分布
　　です。
　3.以下、２種類の木版から合板を作る場合を記載して
　　行きます。
　4.合板を作る手順は、下記の通りです。
　　・木版１をａ枚に切る。
　　・木版２をｂ枚に切る。
　　・木版１×ａ枚＋木版２×ｂ枚を交互に重ねて、
　　　合板を作る。

---

2. 木版１と木版２の組み合わせ

（解説）
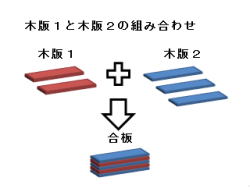
　1.木版１と木版２の組み合わせについて、説明して
　　行きます。
　2.左図の様に、木版１と木版２を交互に重ねます。
　3.木版１は２枚有りますが、２枚とも同じ品質です。
　　即ち、厚さの平均値と分散が同じです。
　4.木版２は３枚有りますが、３枚とも同じ品質です。
　　即ち、厚さの平均値と分散が同じです。
　5.この事例は、部品と部品を組み合わせて製品を作る
　　場合と類似しています。

---

3. 厚さの平均値と分散

（解説）
　1.厚さの平均値と分散について、説明して行きます。
　2.下記に、２つの独立変数を合計した分布の場合を
　　示します。
　3.記号の意味
　　Ｘ_１：独立変数、　ａ：Ｘ_１の定数
　　Ｘ_２：独立変数、　ｂ：Ｘ_２の定数
　4.平均値
　　Ｙ＝ａX_１＋ｂX_２
　5.分散
　　σ_Ｙ^２＝ａ^２σ_Ｘ１^２＋ｂ^２σ_Ｘ２^２

---

4. 合板厚さの推定値

（解説）
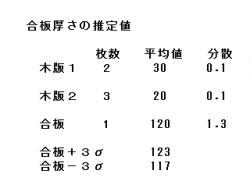
　1.合板厚さの推定値について、説明して行きます。
　2.具体的な数値を入れて、解説します。
　3.木片は、下記を使用します。
　　木片１：　厚さ３０ｍｍを２枚。
　　木片２：　厚さ２０ｍｍを３枚。
　4.合板の平均値及び分散は、木片１と木片２の平均値
　　及び分散から計算します。
　5.合板厚さの推定値は、合板の平均値及び分散から
　　算出します。（合板厚さ±３σ）
　6.想像以上に、バラツキが大きいと感じます。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）