品質管理はデータに始まり、データで終わります。

1. 検定、推定とは

（解説）
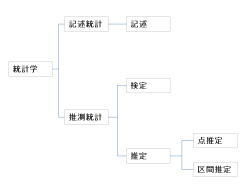
　1.統計学には記述統計と推測統計があります。
　　検定、推定は、推測統計に分類されます。
　2.検定とは、対象となる母集団を仮定して統計的な
　　判断を行うことです。検定を有意差検定と呼ぶ
　　場合も有ります。検定は差が有ることを証明する
　　方法で、差がない事（同じである事）は証明でき
　　ません。品質管理では、感に頼らずデータで事実
　　を判断する事がとても重要です。

　・対象となる特性は、母平均、母分散、平均値の差などです。
　・２つの仮説を設定し、その採否を行います。
　・仮説は、帰無仮説Ｈ_０：μ＝μ_０、対立仮説Ｈ_１：μ≠μ_０の様に設定します。
　・通常は、有意水準α＝５％で検定を行います。
3.推定とは、対象となる母集団を仮定して統計的な推測を行うことです。
　・対象となる特性は、母平均、母分散、平均値の差などです。
　・推定には、点推定と区間推定があります。
　・点推定は、１つの統計量で母数を推定することです。
　・区間推定は、区間をもって母数を推測することで、通常は信頼率１−α＝９５％で行います。

---

2. 母平均（σ既知）

（解説）
　1.母平均の検定について、説明して行きます。
　　推定は割愛します。
　　・前提条件　σ_０は既知、μ_０を指定
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：μ＝μ_０
　　・対立仮説Ｈ_１：μ≠μ_０
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・ｕ検定（両側、上側、下側）

---

3. 母平均（σ未知）

（解説）
　1.母平均の検定について、説明して行きます。
　　推定は割愛します。
　　・前提条件　σ_０は未知、μ_０を指定
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：μ＝μ_０
　　・対立仮説Ｈ_１：μ≠μ_０
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・ｔ検定（両側、上側、下側）

---

4. 母分散

（解説）
　1.母分散の検定について、説明して行きます。
　　推定は割愛します。
　　・前提条件　σ_０を指定
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：σ^２＝σ_０^２
　　・対立仮説Ｈ_１：σ^２≠σ_０^２
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・χ^２検定（両側、上側、下側）

5. 分散の比

（解説）
　1.分散比の検定について、説明して行きます。
　　推定は割愛します。
　　・前提条件　なし
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：σ_１^２＝σ_２^２
　　・対立仮説Ｈ_１：σ_１^２≠σ_２^２
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・F検定（両側、上側、下側）

---

6. 平均値の差（等分散）

（解説）
　1.平均値の差（等分散）の検定について、説明して
　　行きます。推定は割愛します。
　　・前提条件　分散が等しい
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：μ_１＝μ_２
　　・対立仮説Ｈ_１：μ_１≠μ_２
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・ｔ検定（両側、上側、下側）

---

7. 平均値の差（非等分散）

（解説）
　1.平均値の差（非等分散）の検定について、説明して
　　行きます。推定は割愛します。
　　・前提条件　なし
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：μ_１＝μ_２
　　・対立仮説Ｈ_１：μ_１≠μ_２
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・ｔ検定（Ｗｅｌｃｈ）（両側、上側、下側）

---

8. 平均値の差（対応あり）

（解説）
　1.平均値の差（対応あり）の検定について、説明して
　　行きます。推定は割愛します。
　　・前提条件　データが対になっている
　2.仮説設定（両側検定の場合）
　　・帰無仮説Ｈ_０：μ_ｄ＝０
　　・対立仮説Ｈ_１：μ_ｄ≠０
　3.有意水準
　　・α＝５％
　4.統計検定量
　　・図の式を参照

5.棄却域
　・図の式を参照
6.手法
　・ｔ検定（両側、上側、下側）

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）