L9実験計画(交互作用を無視)l9 doe
(目次)
1. L9実験計画(交互作用を無視)とは
2. 直交表への割付け
3. 実験の実施
4. 各水準毎の和を算出
5. 各項目の計算
6. 分散分析表の作成
7. 最適条件の選定と推定
1. L9実験計画(交互作用を無視)とは

(解説)
1.L9実験計画(交互作用を無視)について、
説明して行きます。
2.L9実験計画(交互作用を無視)は、以下の特徴が
有ります。
・目的 : 最適化実験
・実験数: 8回×連続n個
・因子 : 最大4因子
・水準 : 3水準
・割付け: 自由
2. 直交表への割付け
(解説)
1.直交表への割付けについて、説明して行きます。
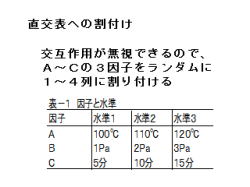
2.因子と水準は、左表1の設定とします。
・因子: 3因子(A〜C)
・水準: 3水準
3.交互作用が無視できるので、A〜Cの3因子を
ランダムに1〜4列に割り付けます。
4.交互作用がある場合は、線点図を用いて割り付け
ますが、今回は使いません。
3. 実験の実施
(解説)
1.実験の実施について、説明して行きます。
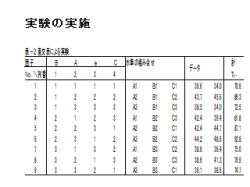
2.左表2に様に実験計画を作成し、実験を実施し
ます。
3.実験の順序は、ランダムに行います。
4.得られた結果を、右列のデータに記載します。
5.本例では同一条件でデータを2個連続で採取する
ので、完全ランダムでは有りません。
4. 各水準毎の和を算出
(解説)
1.各水準毎の和を算出について、説明して行きます。
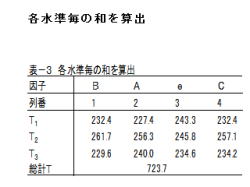
2.左表3の様に、下記の項目を算出します。
・第1水準の和T1
・第2水準の和T2
・第3水準の和T3
・総計T
5. 各項目の計算

(解説)
1.各項目の計算について、説明して行きます。
2.計算する項目を以下に記します。
・修正項 : CT=T2/N=
・総変動 : ST=
・要因変動: SA=
・要因変動: SB=
・要因変動: SC=
・誤差変動: Se1=
・誤差変動: Sew=
・自由度 : fT=N−1=
・自由度 : fA=a−1=
・自由度 : fB=b−1=
・自由度 : fC=c−1=
・自由度 : fe1=
・自由度 : few=
3.記号の補足
・T: 全データの合計
・N: 全データの個数
・a: 水準数
・b: 水準数
・c: 水準数
6. 分散分析表の作成
(解説)
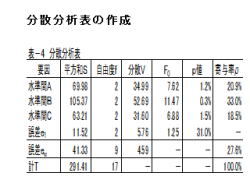
1.分散分析表の作成について、説明して行きます。
2.左表4の様に、分散分析表を作成します。
3.横の項目
・要因
・平方和S
・自由度f
・分散V
・F0
・p値
・寄与率ρ
4.縦の項目
・水準間A
・水準間B
・水準間C
・誤差e1
・誤差ew
・計T
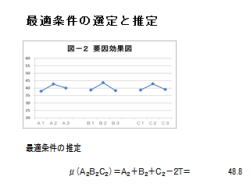
7. 最適条件の選定と推定
(解説)
1.最適条件の選定と推定について、説明します。
2.最適条件の選定
・左図2の様に、要因効果図を作成します。
・A2、B2、C2が最適条件と分かります。
3.最適条件の推定
・下記の計算式で、推定します。
・μ(A2B2C2)=A2+B2+C2−2T=
・ここで、Tは総平均を意味します。
4.上記の推定は大雑把に見えますが、直交実験では
良く用いられます。
品質管理ソフトは、下記をクリックして下さい。
本館:エクセル将棋館(品質管理ソフト)