品質管理はデータに始まり、データで終わります。

1. 分散成分とは

（解説）
　1.分散成分について、説明して行きます。
　2.ここでは、二元配置分散分析（ｎ≧２）の事例を
　　用います。
　3.二元配置のモデルは下記３つが有りますが、
　　モデル�U（変量モデル）について記述します。

　・モデル�T　：　母数モデルとも呼ばれ、要因Ａ、要因Ｂの水準を制御できる場合。
　・モデル�U　：　変量モデルとも呼ばれ、要因Ａ、要因Ｂの水準が制御できない場合。
　・混合モデル：　要因Ａの水準を制御でき、要因Ｂの水準が制御できない場合。

4.分散分析表より求めた分散は、誤差ε_ｉｊｋを含んでいます。
5.分散成分は、分散から誤差ε_ｉｊｋを除いた値です。分散の期待値Ｅ（Ｖ）とも呼ばれます。
6.データは、下記の構造模型で表わせます。
　・ｘ_ｉｊｋ＝μ＋α_ｉ＋β_ｊ＋（αβ）_ｉｊ＋ε_ｉｊｋ
7.分散成分（要因Ａの場合）は、下記の式となります。
　・σ_Ａ^２＝１／（ａ−１）Σα_ｉ^２＝１／（ａ−１）Σ（μ_ｉ−μ）^２

---

2. 要因Ａの分散成分

（解説）
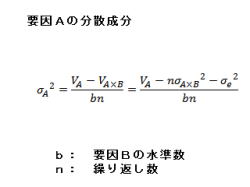
　1.要因Ａの分散成分について、説明して行きます。
　2.Ｖ_ＡからＶ_Ａ×Ｂを引いて、ｂｎで割ります。
　3.要因Ａの分散成分の計算方法は、以下の通りです。
　　・σ_Ａ^２＝（Ｖ_Ａ−Ｖ_Ａ×Ｂ）／ｂｎ
　　　　　　＝（Ｖ_Ａ−ｎσ_Ａ×Ｂ^２−σ_ｅ^２）／ｂｎ
　　・ｂ：　要因Ｂの水準数
　　・ｎ：　繰り返し数

---

3. 要因Ｂの分散成分

（解説）
　1.要因Ｂの分散成分について、説明して行きます。
　2.Ｖ_ＢからＶ_Ａ×Ｂを引いて、ａｎで割ります。
　3.要因Ｂの分散成分の計算方法は、以下の通りです。
　　・σ_Ｂ^２＝（Ｖ_Ｂ−Ｖ_Ａ×Ｂ）／ａｎ
　　　　　　＝（Ｖ_Ｂ−ｎσ_Ａ×Ｂ^２−σ_ｅ^２）／ａｎ
　　・ｂ：　要因Ｂの水準数
　　・ｎ：　繰り返し数

---

4. 交互作用Ａ×Ｂの分散成分

（解説）
　1.交互作用Ａ×Ｂの分散成分について、説明して行き
　　ます。
　2.交互作用Ａ×Ｂの分散成分は、要因Ａの分散成分、
　　要因Ｂの分散成分の計算にも必要です。
　3.Ｖ_Ａ×ＢからＶ_ｅを引いて、ｎで割ります。
　4.交互作用Ａ×Ｂの分散成分の計算方法は、以下の
　　通りです。
　　・σ_Ａ×Ｂ^２＝（Ｖ_Ａ×Ｂ−Ｖ_ｅ）／ｎ
　　　　　　　＝（Ｖ_Ａ×Ｂ−σ_ｅ^２）／ｎ
　　・ｎ：　繰り返し数

5. 誤差ｅの分散成分

（解説）
　1.誤差ｅの分散成分について、説明して行きます。
　2.誤差ｅの分散成分は、要因Ａの分散成分、要因Ｂの
　　分散成分、交互作用Ａ×Ｂの分散成分の計算にも
　　必要です。
　3.誤差分散Ｖ_ｅと同じです。
　4.誤差ｅの分散成分の計算方法は、以下の通りです。
　　・σ_ｅ^２＝Ｖ_ｅ

---

6. 全体の分散成分

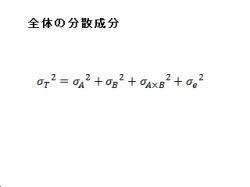
（解説）
　1.全体の分散成分について、説明して行きます。
　2.全ての分散成分の合計となります。
　3.全体の分散成分の計算方法は、以下の通りです。
　　・σ_Ｔ^２＝σ_Ａ^２＋σ_Ｂ^２＋σ_Ａ×Ｂ^２＋σ_ｅ^２

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）