品質管理はデータに始まり、データで終わります。

1. 回帰式とは

（解説）
　1.回帰式について、説明して行きます。
　2.回帰式とは、回帰直線を描く為の数式です。
　3.モデル式を仮定し、回帰式で近似します。
　　・ｙ_ｉ＝β_０＋β_１ｘ_ｉ１＋ε_ｉ
　　・ｙ_ｈａｔ＝β_ｈａｔ０＋β_ｈａｔ１ｘ_１

---

2. 回帰式のパラメータ

（解説）
　1.回帰式のパラメータについて、説明して行きます。
　2.回帰式を作成するには、パラメータを推定する必要
　　が有ります。
　3.パラメータは、β_ｈａｔ０とβ_ｈａｔ１の２つ有り
　　ますが、β_ｈａｔ１を先に求めます。
　4.β_ｈａｔ１の推定（傾き）
　　・β_ｈａｔ１＝Ｓ_ｘｙ／Ｓ_ｘｘ
　5.β_ｈａｔ０の推定（切片）
　　・β_ｈａｔ０＝ｙ_ｂａｒ−β_ｈａｔ１ｘ_ｂａｒ

---

3. エクセル関数でパラメータを算出

（解説）
　1.エクセル関数でパラメータを算出について、説明
　　して行きます。
　2.エクセル関数を用いると、２つのパラメータが推定
　　できます。
　3.β_ｈａｔ１の推定（傾き）
　　・β_ｈａｔ１＝SLOPE(既知の y, 既知の x)
　4.β_ｈａｔ０の推定（切片）
　　・β_ｈａｔ０＝INTERCEPT(既知の y, 既知の x)

---

4. データ表、計算例

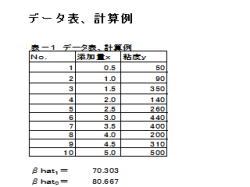
（解説）
　1.データ表、計算例について、説明して行きます。
　2.左表の様に、添加量ｘ、粘度ｙの表を作成し、
　　エクセル関数で計算します。
　3.β_ｈａｔ１の推定（傾き）
　　・β_ｈａｔ１＝SLOPE(既知の y, 既知の x)
　　　＝７０．３０３
　4.β_ｈａｔ０の推定（切片）
　　・β_ｈａｔ０＝INTERCEPT(既知の y, 既知の x)
　　　＝８０．６６７

---

5. 散布図での近似式

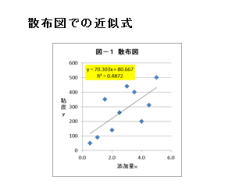
（解説）
　1.散布図での近似式について、説明して行きます。
　2.エクセルの散布図は、近似式を表示ができます。
　3.手順は、以下の通りです。
　　・散布図を作成します。
　　・プロットを選択して、右クリックします。
　　・「近似曲線の追加」を選択します。
　　・「線形近似」、「グラフに数式を表示する」に
　　　チェックを入れると、回帰式が表示されます。
　4.左図の例は、「グラフにＲ−２乗値を表示する」に
　　チェックしてるので、寄与率Ｒ^２も表示です。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）