残差の検討review of residuals
(目次)
1. 残差とは
2. 残差のバラツキ、標準化
3. 標準化偏差の算出
4. 予測値と標準化偏差の散布図
1. 残差とは

(解説)
1.残差について、説明して行きます。
2.残差は、実測値から予測値を引いた値です。
3.残差を数値で表現すると、以下の通りになります。
・残差ei=実測値yi−予測値yhati
4.残差は、左式の様に回帰式を用いて算出します。
5.残差で、回帰式の妥当性を評価します。
2. 残差のバラツキ、標準化

(解説)
1.残差のバラツキ、標準化について、説明して行き
ます。
2.残差で回帰式の妥当性を評価しますが、残差の
バラツキを求め、さらに標準化する必要が有り
ます。
3.残差のバラツキは、分散の平方根から算出します。
(標準偏差)
・σhate=Ve0.5
・ここで、Veを算出する時の自由度φe=n−2
に注意。
4.残差の標準化は、残差を分散の平方根で割ります。(標準化残差)
・ei’=ei/Ve0.5
5.残差の標準化を行う理由は、特性値によって残差の絶対値が大きく変わり、残差そのものでは回帰式の
妥当性が評価できない為です。
3. 標準化偏差の算出
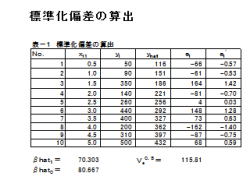
(解説)
1.標準化偏差の算出について、説明して行きます。
2.左表の様に、下記項目を記述及び算出します。
・要因 : xi1
・実測値 : yi
・予測値 : yhati
・残差 : ei
・標準化残差: ei’
3.標準化残差が、−3〜3の間で有れば正常と判断
します。
4. 予測値と標準化偏差の散布図
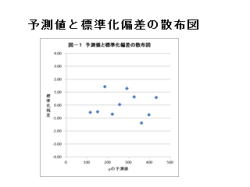
(解説)
1.予測値と標準化偏差の散布図について、説明して
行きます。
2.左図の様に、横軸にyの予測値、縦軸に標準化残差
を取り、散布図を作成します。
3.散布図の見方は、大きくは下記の2つが有ります。
・標準化残差が、−3〜3から外れていないか?
・増加、減少、周期性などの現象はないか?
4.上記の2つで異常が無ければ、回帰式は妥当と判断
します。
品質管理ソフトは、下記をクリックして下さい。
本館:エクセル将棋館(品質管理ソフト)