品質管理はデータに始まり、データで終わります。

1. 説明変数が量的変数

（解説）
　1.説明変数が量的変数について、説明して行きます。
　2.説明変数が量的変数は、以下を検討します。
　　・データ
　　・単純な回帰分析による解析
　　・経験ロジット
　　・経験ロジットを用いた回帰分析
　　・逆ロジット変換
　3.変数は、以下の通りです。
　　・目的変数：　質的変数
　　・説明変数：　量的変数

---

2. データ

（解説）
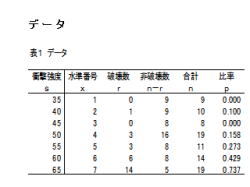
　1.データについて、説明して行きます。
　2.左表は、衝撃強度を変化させた時の破壊比率を調査
　　した結果です。
　3.表の構成は、以下の通りです。
　　・衝撃強度：　ｓ
　　・水準番号：　ｘ
　　・破壊数　：　ｒ
　　・非破壊数：　ｎ−ｒ
　　・合計　　：　ｎ
　　・比率　　：　ｐ

4.衝撃強度ｓと水準番号ｘの関係は、以下の通りです。
　・ｘ＝（ｓ−３０）／５

---

3. 単純な回帰分析による解析

（解説）
　1.単純な回帰分析による解析について、説明して
　　行きます。
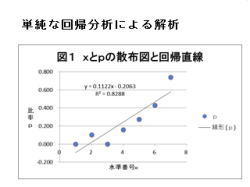
　2.単純な回帰分析では、下記の回帰式となります。
　　・ｙ＝０．１１２２ｘ−０．２０６３
　3.上記の回帰式では、予測値が０〜１の範囲外になる
　　ので、好ましく有りません。

---

4. 経験ロジット

（解説）
　1.経験ロジットについて、説明して行きます。
　2.比率の回帰分析は、ロジット変換が有用です。
　3.しかし、ｒ＝０又ははｎ（破壊無し、破壊全て）の
　　場合は、ｚが−∞又は＋∞になります。
　4.そこで、左式上部の様に修正します。
　5.左式下部を経験ロジットと呼びます。

---

5. 経験ロジットを用いた回帰分析

（解説）
　1.経験ロジットを用いた回帰分析について、説明して
　　行きます。
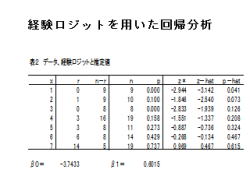
　2.左表は、データ、経験ロジットと推定値です。
　3.表の構成は、以下の通りです。
　・水準番号 ：　ｘ
　・破壊数　 ：　ｒ
　・非破壊数 ：　ｎ−ｒ
　・合計　　 ：　ｎ
　・比率　　 ：　ｐ
　・経験ﾛｼﾞｯﾄ：　ｚ＊

　・ｚ推定値 ：　ｚ−ｈａｔ
　・ｐ推定値 ：　ｐ−ｈａｔ
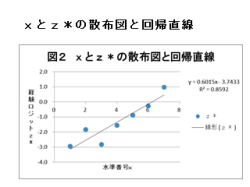
4.回帰式は、ｘとｚ＊より求めます。
　これは、ロジスティック回帰式と呼びます。
5.ｚ−ｈａｔは、回帰式より計算します。
6.ｐ−ｈａｔは、次項の逆ロジット変換より算出し
　ます。
7.左図は、ｘとｚ＊の散布図と回帰直線となります。

---

6. 逆ロジット変換

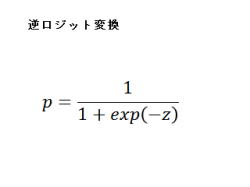
（解説）
　1.逆ロジット変換について、説明して行きます。
　2.左式は、ロジットｚから比率ｐを求める式です。
　3.この事を逆ロジット変換と言います。

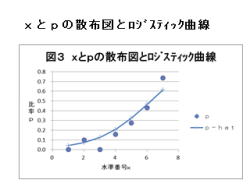
　4.左図は、ｘとｐの散布図とロジスティック曲線と
　　なります。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）