品質管理はデータに始まり、データで終わります。

1. ロジスティック重回帰

（解説）
　1.ロジスティック重回帰について、説明して行き
　　ます。
　2.ロジスティック重回帰は、以下を検討します。
　　・データ
　　・ｘ_２とｐ及びｘ_２とｚ＊の関係
　　・考え方
　　・ロジスティック重回帰分析
　　・ロジスティック曲線の当てはめ
　3.ロジスティック重回帰は、説明変数が２つ以上に
　　なります。

4.変数は、以下の通りです。
　・目的変数：　質的変数
　・説明変数：　質的変数、量的変数

---

2. データ

（解説）
　1.データについて、説明して行きます。
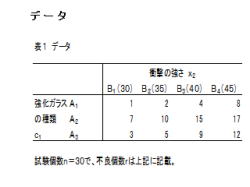
　2.左表は、強化ガラスの種類、衝撃の強さを変化
　　させた時の不良個数を調査したものです。
　3.表の構成は、以下の通りです。
　　・強化ガラスの種類ｃ_１：　Ａ_１、Ａ_２、Ａ_３
　　・衝撃の強さ　　　ｘ_２：　Ｂ_１、Ｂ_２、Ｂ_３
　　・試験個数ｎ＝３０で、不良個数ｒを記載。
　4.以下、解析手順を記載して行きます。

---

3. ｘ２とｐ及びｘ２とｚ＊の関係

（解説）
　1.ｘ_２とｐ及びｘ_２とｚ＊の関係について、説明して
　　行きます。
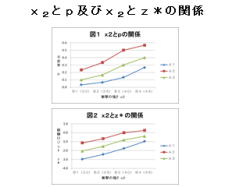
　2.図１は、ｘ_２とｐの関係を示しています。
　　・ｘ_２：　衝撃の強さ
　　・ｐ　：　不良率
　3.図２は、ｘ_２とｚ＊の関係を示しています。
　　・ｘ_２：　衝撃の強さ
　　・ｚ＊：　経験ロジット
　4.図１は交互作用が有り、図２は交互作用が無い様に
　　見えます。この理由は、次項で説明します。

---

4. 考え方

（解説）
　1.考え方について、説明して行きます。
　2.不良率ｐの場合は、加法性が成立しません。
　　・ｌｎを使用すると、加法性が成立します。
　　・ｐが小さい：　ln(p)
　　・ｐが大きい：　-ln(1-p)
　3.ロジットｚの場合は、加法性が成立します。
　　・z=ln(p)-ln(1-p)=ln(p/(1-p))
　4.経験ロジットｚ＊は、ロジットｚと同じです。
　5.この様にして加法性の問題で、交互作用の有無が
　　発生します。

---

5. ロジスティック重回帰分析

（解説）
　1.ロジスティック重回帰分析について、説明して
　　行きます。
　2.ｃ_１は質的変数なので、ダミー変数に変換して
　　解析します。
　3.左式は、経験ロジットｚ＊の回帰式となります。

---

6. ロジスティック曲線の当てはめ

（解説）
　1.ロジスティック曲線の当てはめについて、説明して
　　行きます。
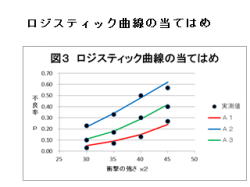
　2.左図は、観測されたｐとその推定値ｐ−ｈａｔの
　　グラフです。
　　・横軸：　衝撃強さ　ｘ_２
　　・縦軸：　不良率　　ｐ、ｐ−ｈａｔ

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）