品質管理はデータに始まり、データで終わります。

1. 説明変数の追加で残差平方和が減少

（解説）
　1.説明変数の追加で残差平方和が減少について、説明
　　して行きます。
　2.説明変数を追加する事で、予測式が改善するか
　　どうかを調べる必要が有ります。
　3.説明変数を追加すると、必ず残差平方和が減少し
　　ます。
　　・変数一つ：Ｓ_ｅ＝１７．８１６
　　・変数二つ：Ｓ_ｅ＝　７．６５４
　4.従って、説明変数の追加により、どの程度に残差
　　平方和が減少したかが重要となります。

---

2. Ｆ比（分散比）の算出

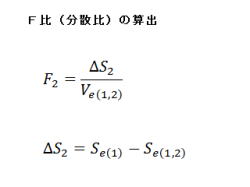
（解説）
　1.Ｆ比（分散比）の算出について、説明して行き
　　ます。
　2.左式の上段が、Ｆ比（分散比）となります。
　　・Ｆ_２＝ΔＳ_２／Ｖ_{ｅ（１，２）}
　3.左式の下段が、残差平方和の変化量です。
　　・ΔＳ_２＝Ｓ_ｅ（１）−Ｓ_{ｅ（１，２）}

---

3. Ｆ比の目安

（解説）
　1.Ｆ比の目安について、説明して行きます。
　2.説明変数を追加するかどうかは、Ｆ比が目安です。
　3.Ｆ≦２
　　・変数を追加しません。
　4.Ｆ≧Ｆ（１，ｆ_{ｅ（１，２）}；０．０５）
　　・変数を追加します。
　5.２≦Ｆ≦Ｆ（１，ｆ_{ｅ（１，２）}；０．０５）
　　・固有技術の知識を含め、総合的に判断します。
　6.Ｆ比が大きい説明変数は、重回帰式で有効な役割を
　　果たしています。

---

4. 平方和の注意事項

（解説）
　1.平方和の注意事項について、説明して行きます。
　2.左式の上段の様に、説明変数の追加による平方和は
　　異なります。
　　・Ｓ_Ｒ（１）≠ΔＳ_１
　　・Ｓ_Ｒ（２）≠ΔＳ_２
　3.重回帰式で説明できる平方和は、左式の下段の様に
　　２通りの分割が考えられます。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）