品質管理はデータに始まり、データで終わります。

1. 中心極限定理とは

（解説）
　1.中心極限定理について、説明して行きます。
　2.中心極限定理は、以下の通りです。
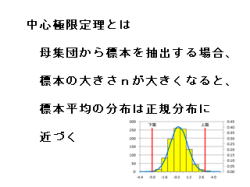
　　・母集団から標本を抽出する場合、標本の大きさ
　　　ｎが大きくなると、標本平均の分布は正規分布
　　　に近づく。
　3.正規分布は、左図の右下となります。
　4.以下、代表的分布に対し、エクセルＶＢＡで検証
　　（シミュレーション）した結果を示します。

---

2. 一様分布で検証

（解説）
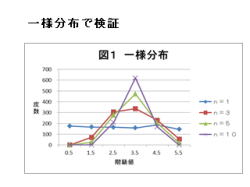
　1.一様分布で検証について、説明して行きます。
　2.一様分布で、以下の条件にて検証しました。
　　・エクセル関数：　=RANDBETWEEN(1,6)
　　・標本の大きさ：　ｎ＝１、３、５、１０
　　・標本の数　　：　ｋ＝１０００
　　・標本平均　　：　Ｘｂａｒ_ｎ
　3.標本の大きさｎが大きくなると、標本平均の分布
　　は正規分布に近づきます。

---

3. 正規分布で検証

（解説）
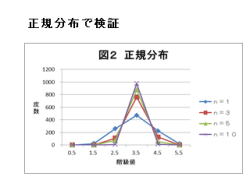
　1.正規分布で検証について、説明して行きます。
　2.正規分布で、以下の条件にて検証しました。
　　・エクセル関数：
　　　=ROUND(NORM.INV(RAND(),3.5,0.75),1)
　　・標本の大きさ：　ｎ＝１、３、５、１０
　　・標本の数　　：　ｋ＝１０００
　　・標本平均　　：　Ｘｂａｒ_ｎ
　3.標本の大きさｎが大きくなると、標本平均の分布
　　は正規分布に近づきます。

---

4. 二項分布で検証

（解説）
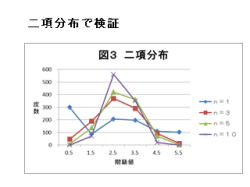
　1.二項分布で検証について、説明して行きます。
　2.二項分布で、以下の条件にて検証しました。
　　・エクセル関数：　=ROUND(
　　　BINOM.INV(INT(RAND()*10),0.5,0.75),1)
　　・標本の大きさ：　ｎ＝１、３、５、１０
　　・標本の数　　：　ｋ＝１０００
　　・標本平均　　：　Ｘｂａｒ_ｎ
　3.標本の大きさｎが大きくなると、標本平均の分布
　　は正規分布に近づきます。

---

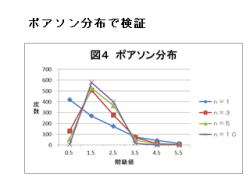
5. ポアソン分布で検証

（解説）
　1.ポアソン分布で検証について、説明して行きます。
　2.ポアソン分布で、以下の条件にて検証しました。
　　・エクセル関数：
　　　=ROUND(GAMMA.INV(RAND(), 2, 1), 0)
　　・標本の大きさ：　ｎ＝１、３、５、１０
　　・標本の数　　：　ｋ＝１０００
　　・標本平均　　：　Ｘｂａｒ_ｎ
　3.標本の大きさｎが大きくなると、標本平均の分布
　　は正規分布に近づきます。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）