品質管理はデータに始まり、データで終わります。

1. 変数変換とは

（解説）
　1.変数変換について、説明して行きます。
　2.変数変換は、関数を使って元の数値を変換する方法
　　です。
　3.散布図では横軸に変数ｘ、縦軸に変数ｙを採る事に
　　よって、変数ｘと変数ｙの相関を調べられます。
　　この時、直線関係が無い事がしばしば有ります。
　4.しかし、変数ｙを変数変換する事で相関が得られる
　　場合が有ります。
　5.この様に変数変換は、正しい相関を調べる為に有用
　　な手法です。

---

2. 平方根変換

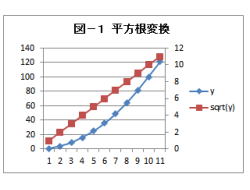
（解説）
　1.平方根変換について、説明して行きます。
　2.変数ｙが２次関数の時に、平方根変換を行います。
　3.２次関数は、下式で表されます。
　　ｙ＝ａｘ^２＋ｂ
　4.これの平方根を取ると、ｘの１次関数になります。
　5.平方根変換は、下記の関数で行います。
　　ｆ（ｙ）＝ｓｑｒｔ（ｙ）

---

3. ２乗変換

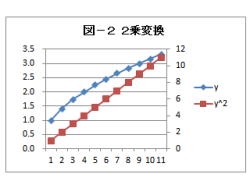
（解説）
　1.２乗変換について、説明して行きます。
　2.変数ｙが平方根関数の時に、２乗変換を行います。
　3.平方根関数は、下式で表されます。
　　ｙ＝ｓｑｒｔ（ａｘ＋ｂ）
　4.これの２乗を取ると、ｘの１次関数になります。
　5.２乗変換は、下記の関数で行います。
　　ｆ（ｙ）＝ｙ^２

---

4. 対数変換

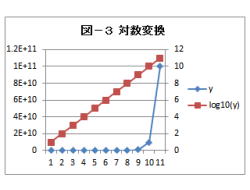
（解説）
　1.対数変換について、説明して行きます。
　2.変数ｙが指数関数の時に、対数変換を行います。
　3.指数関数は、下式で表されます。
　　ｙ＝１０^ａｘ＋ｂ
　4.これの対数を取ると、ｘの１次式になります。
　5.対数変換は、下記の関数で行います。
　　ｆ（ｙ）＝ｌｏｇ_１０（ｙ）

---

5. 指数変換

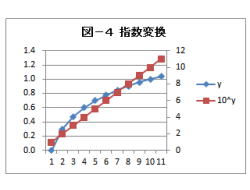
（解説）
　1.指数変換について、説明して行きます。
　2.変数ｙが対数関数の時に、指数変換を行います。
　3.対数関数は、下式で表されます。
　　ｙ＝ｌｏｇ_１０（ａｘ＋ｂ）
　4.これの指数を取ると、ｘの１次式になります。
　5.指数変換は、下記の関数で行います。
　　ｆ（ｙ）＝１０^ｙ

---

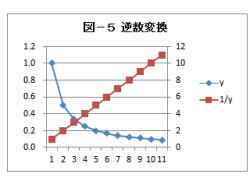
6. 逆数変換

（解説）
　1.逆数変換について、説明して行きます。
　2.変数ｙが逆数関数の時に、逆数変換を行います。
　3.逆数関数は、下式で表されます。
　　ｙ＝１／ｘ
　4.これの逆数を取ると、ｘの１次式になります。
　5.逆数変換は、下記の関数で行います。
　　ｆ（ｙ）＝１／ｙ

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）