品質管理はデータに始まり、データで終わります。

1. 二元配置実験（ｎ≧２）とは

（解説）
　1.二元配置実験（ｎ≧２）について、説明します。
　2.二元配置実験（ｎ≧２）は、因子が２つの実験計画
　　法で、繰返しはｎ回（ｎ≧２）です。
　3.二元配置実験（ｎ≧２）は、以下の組み合せで
　　実験します。
　　・因子：　Ａ、Ｂ
　　・水準：　1,2,3・・・,a (b)
　　・繰返：　ｎ回（ｎ≧２）
　　・順序：　ランダム
　4.以下、計算方法等を記載します。

---

2. 二元配置実験（ｎ≧２）の具体例

（解説）
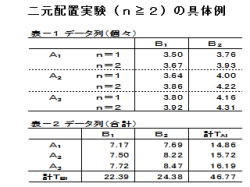
　1.二元配置実験（ｎ≧２）の具体例について、説明。
　2.左表１の様に、データ列を作成します。
　　・左列：　要因Ａ、水準、繰返ｎ
　　・中列：　要因Ｂと水準
　3.繰返ｎを合計して、左表２を作成します。
　　・左列：　要因Ａ、水準
　　・中列：　要因Ｂと水準
　　・右列：　要因Ａで各水準の合計
　　・下行：　要因Ｂで各水準の合計
　4.この表を基にして、各種計算を行います。

---

3. 各要因の変動と自由度を算出

（解説）
　1.各要因の変動と自由度を算出について、説明して
　　行きます。
　2.計算する項目を以下に記します。
　　・修正項　：　ＣＴ＝Ｔ^２／Ｎ＝
　　・総変動　：　Ｓ_Ｔ＝
　　・要因変動：　Ｓ_Ａ＝
　　・要因変動：　Ｓ_Ｂ＝
　　・要因変動：　Ｓ_ＡＢ＝
　　・要因変動：　Ｓ_Ａ×Ｂ＝Ｓ_ＡＢ−Ｓ_Ａ−Ｓ_Ｂ＝

　・誤差変動：　Ｓ_ｅ＝Ｓ_Ｔ−Ｓ_Ａ−Ｓ_Ｂ−Ｓ_Ａ×Ｂ＝
　・自由度　：　ｆ_Ｔ＝ａｂｎ−１＝
　・自由度　：　ｆ_Ａ＝ａ−１＝
　・自由度　：　ｆ_Ｂ＝ｂ−１＝
　・自由度　：　ｆ_ＡＢ＝ａｂ−１＝
　・自由度　：　ｆ_Ａ×Ｂ＝ｆ_ＡＢ−ｆ_Ａ−ｆ_B＝
　・自由度　：　ｆ_ｅ＝ｆ_Ｔ−ｆ_Ａ−ｆ_Ｂ−ｆ_Ａ×Ｂ＝
3.記号の補足
　・Ｔ：　全データの合計
　・Ｎ：　全データの個数
　・ａ：　水準数
　・ｂ：　水準数
　・ｎ：　繰返数

---

4. 分散分析表の作成

（解説）
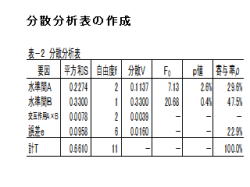
　1.分散分析表の作成について、説明して行きます。
　2.左表の様に、分散分析表を作成します。
　3.横の項目
　　・要因
　　・平方和Ｓ
　　・自由度ｆ
　　・分散Ｖ
　　・Ｆ_０
　　・ｐ値
　　・寄与率ρ

4.縦の項目
　・水準間Ａ
　・水準間Ｂ
　・交互作用Ａ×Ｂ
　・誤差ｅ
　・計Ｔ

---

5. 平均値の推定

（解説）
　1.平均値の推定について、説明して行きます。
　2.有意な因子が異なると、計算方法も違います。
　3.平均値の推定（Ａが有意）
　　・ｘｂａｒ_Ａ１＝（平均値）±
　　　ｔ（ｆ_ｅ，０．０５）×（Ｖ_ｅ／ｂｎ）^０．５
　4.平均値の推定（Ａ、Ｂが有意）
　　・ｘｂａｒ_Ａ３B２＝（平均値）±
　　　ｔ（ｆ_ｅ，０．０５）×
　　　（（ａ＋ｂ−１）Ｖ_ｅ／ａｂｎ）^０．５

5.平均値の推定（Ａ、Ｂ、Ａ×Ｂが有意）
　・ｘｂａｒ_Ａ３Ｂ２＝（平均値）±ｔ（ｆ_ｅ，０．０５）×（Ｖ_ｅ／ｎ）^０．５

---

6. 平均値の差、個々のデータの推定

（解説）
　1.平均値の差、個々のデータの推定について、説明
　　して行きます。
　2.平均値の差、個々のデータの推定は、以下の計算で
　　行います。
　3.平均値の差の推定
　　・ｘｂａｒ_Ａ３Ｂ２−ｘｂａｒ_Ａ２Ｂ２＝
　　　（平均値の差）±ｔ（ｆ_ｅ，０．０５）×
　　　（Ｖ_ｅ／ｎ_ｄ）^０．５

4.個々のデータの存在範囲
　・ｘ_Ａ１＝（平均値）±ｔ（ｆ_ｅ，０．０５）×（（１＋１／ｎ_ｅ）Ｖ_ｅ）^０．５

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）