品質管理はデータに始まり、データで終わります。

1. 故障、寿命の確率分布　ｔ、ｆ（ｔ）

（解説）
　1.故障、寿命の確率分布　ｔ、ｆ（ｔ）について、
　　説明して行きます。
　2.サンプルは、非修理系と修理系に分類できます。
　　以下、サンプルは製品と読み替えても構いません。
　　・非修理系：　故障すると修理が出来ない。
　　・修理系　：　故障しても修理が出来る。
　3.以下、非修理系について記載します。
　4.信頼性は、「動作時間に対する故障･寿命の確率
　　分布」で表現できます。

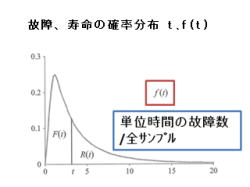
5.横軸に動作時間ｔ、縦軸に確率密度関数ｆ（ｔ）を記載した確率分布が、信頼性を表します。
6.確率密度関数ｆ（ｔ）は、単位時間当たりの故障数です。
7.故障、寿命の確率分布は、故障数のヒストグラムを同じ形となります。

---

2. 信頼度Ｒ（ｔ）

（解説）
　1.信頼度Ｒ（ｔ）について、説明して行きます。
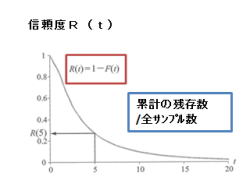
　2.信頼度Ｒ（ｔ）は、動作時間ｔにおける、累計の
　　残存数／全サンプル数で表せます。
　3.信頼度Ｒ（ｔ）は、不信頼度Ｆ（ｔ）と下記の関係
　　に有ります。
　　・信頼度：　Ｒ（ｔ）＝１−Ｆ（ｔ）
　4.信頼度Ｒ（ｔ）は、その時点で稼働している
　　サンプルの比率です。
　5.例えば、Ｒ（１年）＝５０％だと、１年後に稼働
　　しているサンプルは５０％が予想されます。

---

3. 故障率λ（ｔ）

（解説）
　1.故障率λ（ｔ）について、説明して行きます。
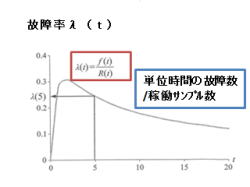
　2.故障率λ（ｔ）は、動作時間ｔにおける、単位時間
　　の故障数／稼働サンプル数で表せます。
　3.故障率λ（ｔ）は、確率密度関数ｆ（ｔ）を信頼度
　　Ｒ（ｔ）で割ると得られます。
　　・λ（ｔ）＝ｆ（ｔ）／Ｒ（ｔ）
　4.故障率λ（ｔ）は、その時点で稼働している
　　サンプルの故障率です。
　5.分母が全サンプルでは無く、稼働しているサンプル
　　である事に注意して下さい。

---

4. 不信頼度Ｆ（ｔ）

（解説）
　1.不信頼度Ｆ（ｔ）について、説明して行きます。
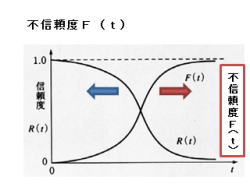
　2.不信頼度Ｆ（ｔ）は、累積故障率とも呼ばれます。
　3.不信頼度Ｆ（ｔ）は、信頼度Ｒ（ｔ）と逆の関係に
　　有ります。
　　・Ｆ（ｔ）＝１−Ｒ（ｔ）

---

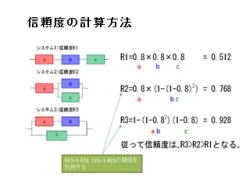
5. 信頼度の計算方法

（解説）
　1.信頼度の計算方法について、説明して行きます。
　2.信頼度は、直列、並列システムで計算方法が異なり
　　ます。
　3.ユニットａ、ｂ、ｃの信頼度α＝０．８と仮定した
　　場合、各システムの信頼度は下記の通りです。
　　・Ｒ１＝０．８×０．８×０．８＝０．５１２
　　・Ｒ２＝０．８×（１−（１−０．８）^２）
　　　　　＝０．７６８
　　・Ｒ３＝１−（１−０．８^２）（１−０．８）
　　　　　＝０．９２８

4.従って信頼度は、Ｒ３＞Ｒ２＞Ｒ１となります。
5.計算には、Ｒ（ｔ）＝１−Ｆ（ｔ）、Ｆ（ｔ）＝１−Ｒ（ｔ）の関係を利用します。

---

6. ＭＴＴＦ（平均故障時間）

（解説）
　1.ＭＴＴＦ（平均故障時間）について、説明して
　　行きます。
　2.ＭＴＴＦ（平均故障時間）は、故障率が一定の場合
　　、動作時間を故障数で割って算出できます。
　　・ＭＴＴＦ＝（動作時間）／（故障数）　
　3.「サンプルは、何時間使用したら故障するのか？」
　　の目安となります。

---

7. Ｂ１０ライフ

（解説）
　1.Ｂ_１０ライフについて、説明して行きます。
　2.Ｂ_１０ライフは、サンプルの１０％が故障する時間
　　です。
　3.数学的には、Ｆ（ｔ）＝０．１の解で与えられ
　　ます。
　4.多くの製品において､品質保証期間の一つの目安と
　　されています。
　5.Ｂ_１０ライフ＝１年間の場合、１年間でサンプルの
　　１０％が故障します。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）