品質管理はデータに始まり、データで終わります。

1. 異常判定ルールの確率とは

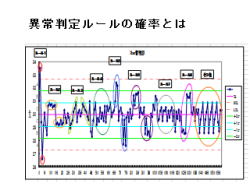
（解説）
　1.異常判定ルールの確率について、説明して行き
　　ます。
　2.工程が安定しているかどうかは、異常判定ルールに
　　より判断します。
　3.異常判定ルールの定義は有りますが、その確率を
　　記載している情報は少ないです。
　4.ここでの確率は、有意水準（危険率）αで、第１種
　　の過誤（あわて者の誤り）です。

5.以下の８つのルールについて解説して行きます。
　・ルール１：　１点が管理限界線（領域Ａ）を超えている。（１点）
　・ルール２：　連が現れる。（７連）
　・ルール３：　上昇傾向、下降傾向が現れる。（６点連続）
　・ルール４：　交互に上下する点が現れる。（１４点連続）
　・ルール５：　管理限界線（領域Ａ）に接近する点が、しばしば現れる。（３点中２点）
　・ルール６：　領域Ｂ又はそれを超えた領域に点が集まる。（５点中４点）
　・ルール７：　中心線の近くに多くの点が集まっている。（１５点連続）
　・ルール８：　領域Ｃを超えた所に多くの点が集まっている。（８点連続）
6.理論確率と実践確率を記載しています。実践確率は、エクセルＶＢＡで１０００×１０００＝１０万回
　のシミュレートした結果です。

---

2. ルール１の確率

（解説）
　1.ルール１の確率について、説明して行きます。
　2.確率の定義
　　・１点が管理限界線（領域Ａ）を超えている。
　　　（１点）
　3.確率の計算式
　　・二項分布関数ｆ（ｘ）＝_ｎＣ_ｘ・ｐ^ｘ・ｑ^ｎ−ｘ
　　　を用いて計算します。
　　　ｎ＝１、ｘ＝１
　　　ｐ＝０．００２７
　　　ｑ＝０．９９７３

　・正規分布の両側確率（±３σ外）＝０．２７％を利用して算出します。
　・エクセル関数：　=BINOMDIST(1,1,0.0027,FALSE)
4.検証結果
　・理論確率：　０．２７％
　・実践確率：　０．２６％

---

3. ルール２の確率

（解説）
　1.ルール２の確率について、説明して行きます。
　2.確率の定義
　　・連が現れる。（７連）
　3.確率の計算式
　　・二項分布関数ｆ（ｘ）＝_ｎＣ_ｘ・ｐ^ｘ・ｑ^ｎ−ｘ
　　　を用いて計算します。
　　　ｎ＝７、ｘ＝７
　　　ｐ＝０．５０００
　　　ｑ＝０．５０００

　・正規分布の片側確率＝５０．００％を利用して算出します。
　・エクセル関数：　=BINOMDIST(7,7,0.5000,FALSE)
4.検証結果
　・理論確率：　０．７８％
　・実践確率：　０．７８％

---

4. ルール３の確率

（解説）
　1.ルール３の確率について、説明して行きます。
　2.確率の定義
　　・上昇傾向、下降傾向が現れる。（６点連続）
　3.確率の計算式
　　・計算式は不明です。
　　　f(x)=不明
　4.検証結果
　　・理論確率：　不明
　　・実践確率：　０．１４％

---

5. ルール４の確率

（解説）
　1.ルール４の確率について、説明して行きます。
　2.確率の定義
　　・交互に上下する点が現れる。（１４点連続）
　3.確率の計算式
　　・計算式は不明です。
　　　f(x)=不明
　4.検証結果
　　・理論確率：　不明
　　・実践確率：　０．４６％

---

6. ルール５の確率

（解説）
　1.ルール５の確率について、説明して行きます。
　2.確率の定義
　　・管理限界線（領域Ａ）に接近する点が、しばしば
　　　現れる。（３点中２点）
　3.確率の計算式
　　・二項分布関数ｆ（ｘ）＝_ｎＣ_ｘ・ｐ^ｘ・ｑ^ｎ−ｘ
　　　を用いて計算します。
　　　ｎ＝３、ｘ＝２
　　　ｐ＝０．０４５５
　　　ｑ＝０．９５４５

　・正規分布の両側確率（±２σ外）＝４．５５％を利用して算出します。
　・エクセル関数：　=BINOMDIST(2,3,0.0455,FALSE)
　・２点が±２σ外になるパターンは４通り有り、２点とも同じ側になるのは２通りなので、最後に２／４
　　を掛けます。
4.検証結果
　・理論確率：　０．３０％
　・実践確率：　０．３１％

---

7. ルール６の確率

（解説）
　1.ルール６の確率について、説明して行きます。
　2.確率の定義
　　・領域Ｂ又はそれを超えた領域に点が集まる。
　　　（５点中４点）
　3.確率の計算式
　　・二項分布関数ｆ（ｘ）＝_ｎＣ_ｘ・ｐ^ｘ・ｑ^ｎ−ｘ
　　　を用いて計算します。
　　　ｎ＝５、ｘ＝４
　　　ｐ＝０．３１７３
　　　ｑ＝０．６８２７

　・正規分布の両側確率（±１σ外）＝３１．７３％を利用して算出します。
　・エクセル関数：　=BINOMDIST(4,5,0.3173,FALSE)
　・４点が±１σ外になるパターンは１６通り有り、４点とも同じ側になるのは２通りなので、最後に
　　２／１６を掛けます。
4.検証結果
　・理論確率：　０．４３％
　・実践確率：　０．５２％

---

8. ルール７の確率

（解説）
　1.ルール７の確率について、説明して行きます。
　2.確率の定義
　　・中心線の近くに多くの点が集まっている。
　　　（１５点連続）
　3.確率の計算式
　　・二項分布関数ｆ（ｘ）＝_ｎＣ_ｘ・ｐ^ｘ・ｑ^ｎ−ｘ
　　　を用いて計算します。
　　　ｎ＝１５、ｘ＝１５
　　　ｐ＝０．６８２７
　　　ｑ＝０．３１７３

　・正規分布の両側確率（±１σ内）＝６８．２７％を利用して算出します。
　・エクセル関数：　=BINOMDIST(15,15,0.6827,FALSE)
4.検証結果
　・理論確率：　０．２７％
　・実践確率：　０．２６％

---

9. ルール８の確率

（解説）
　1.ルール８の確率について、説明して行きます。
　2.確率の定義
　　・領域Ｃを超えた所に多くの点が集まっている。
　　　（８点連続）
　3.確率の計算式
　　・二項分布関数ｆ（ｘ）＝_ｎＣ_ｘ・ｐ^ｘ・ｑ^ｎ−ｘ
　　　を用いて計算します。
　　　ｎ＝８、ｘ＝８
　　　ｐ＝０．３１７３
　　　ｑ＝０．６８２７

　・正規分布の両側確率（±１σ外）＝３１．７３％を利用して算出します。
　・エクセル関数：　=BINOMDIST(8,8,0.3173,FALSE)
4.検証結果
　・理論確率：　０．２７％
　・実践確率：　０．２６％

---

10. 検証結果

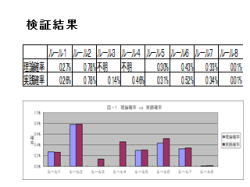
（解説）
　1.検証結果について、説明して行きます。
　2.実践確率は、エクセルＶＢＡで１０００×１０００
　　＝１０万回のシミュレートした結果です。
　3.結果を左記に示しますが、理論確率と実践確率は
　　概ね一致しました。
　4.有意水準（危険率）αは、１％以下となる様です。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）