品質管理はデータに始まり、データで終わります。

1. 系列相関とは

（解説）
　1.系列相関について、説明して行きます。
　2.系列相関は、２変数間の相関関係を簡便に把握する
　　方法です。
　3.系列相関には、大波の相関、小波の相関の２つが
　　有ります。
　　・大波の相関：　データ全体の傾向を見ます。
　　・小波の相関：　１つ前の影響度を見ます。
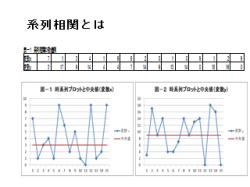
　4.まず、左表の様に、上段に変数ｘ、下段に変数ｙの
　　表を作成します。

5.次に、変数ｘと中央値、変数ｙと中央値のグラフを作ります。

---

2. 大波の相関

（解説）
　1.大波の相関について、説明して行きます。
　2.大波の相関は、データ全体の傾向を見る時に使用
　　します。
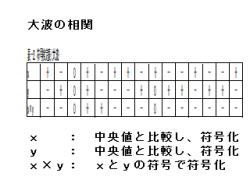
　3.左表の様に、符号検定表（大波）を作成します。
　4.ｘは中央値と比較し、下記の様に符号化します。
　　・大きい場合：　＋
　　・小さい場合：　−
　　・同じ場合　：　０

5.ｙは中央値と比較し、下記の様に符号化します。
　・大きい場合：　＋
　・小さい場合：　−
　・同じ場合　：　０
6.ｘ×ｙは、ｘとｙの符号で符号化します。
　・ｘ、ｙが＋＋又は−−の場合：　＋
　・ｘ、ｙが＋−又は−＋の場合：　−
　・ｘ、ｙに０がある場合　　　：　０
7.ｘ×ｙの符号を、下記の様に数えます。
　・ｎ_＋　　：　＋の数を数えます。（ｎ_＋＝２）
　・ｎ₋　　：　−の数を数えます。（ｎ₋＝１１）
　・Ｎ　　　：　ｎ_＋とｎ₋を合計します。（Ｎ＝１３）
　・ｎ_ｍｉｎ ：　ｎ_＋とｎ₋の小さい方とします。（ｎ_ｍｉｎ＝２）
8.後述する符号検定表（二項分布を利用）より判定を行います。
　・Ｎ＝１３、ｎ_ｍｉｎ＝２なので、有意水準α＝０．０５の棄却領域＝２です。
　・ｎ_ｍｉｎ（２）＜＝棄却領域（２）が成立します。
　・よって、有意水準α＝０．０５で有意（相関あり）となります。

---

3. 小波の相関

（解説）
　1.小波の相関について、説明して行きます。
　2.小波の相関は、１つ前のデータの影響度を見る時に
　　使用します。
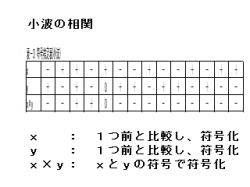
　3.左表の様に、符号検定表（小波）を作成します。
　4.ｘは１つ前のデータと比較し、下記の様に符号化し
　　ます。
　　・大きい場合：　＋
　　・小さい場合：　−
　　・同じ場合　：　０

5.ｙは１つ前のデータと比較し、下記の様に符号化します。
　・大きい場合：　＋
　・小さい場合：　−
　・同じ場合　：　０
6.ｘ×ｙは、ｘとｙの符号で符号化します。
　・ｘ、ｙが＋＋又は−−の場合：　＋
　・ｘ、ｙが＋−又は−＋の場合：　−
　・ｘ、ｙに０がある場合　　　：　０
7.ｘ×ｙの符号を、下記の様に数えます。
　・ｎ_＋　　：　＋の数を数えます。（ｎ_＋＝２）
　・ｎ₋　　：　−の数を数えます。（ｎ₋＝１１）
　・Ｎ　　　：　ｎ_＋とｎ₋を合計します。（Ｎ＝１３）
　・ｎ_ｍｉｎ ：　ｎ_＋とｎ₋の小さい方とします。（ｎ_ｍｉｎ＝２）
8.後述する符号検定表（二項分布を利用）より判定を行います。
　・Ｎ＝１３、ｎ_ｍｉｎ＝２なので、有意水準α＝０．０５の棄却領域＝２です。
　・ｎ_ｍｉｎ（２）＜＝棄却領域（２）が成立します。
　・よって、有意水準α＝０．０５で有意（相関あり）となります。

---

4. 符号検定表（二項分布を利用）

（解説）
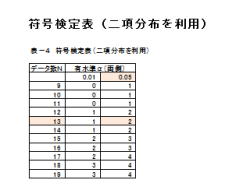
　1.符号検定表（二項分布を利用）について、説明して
　　行きます。
　2.符号検定表（二項分布を利用）は、エクセル関数
　　ＢＩＮＯＭ．ＩＮＶで作成できます。
　　・この時、データ数Ｎ、発生確率（０．５）、
　　　有意水準αを指定します。
　　・棄却領域＝BINOM.INV(ﾃﾞｰﾀ数,0.5,α/2)-1
　　・上記の式は、両側検定の場合となります。

3.上記の通り、エクセル関数ＢＩＮＯＭ．ＩＮＶを使用すれば、データ数、有意水準αを自由に設定でき
　色々な場合の符号検定が可能となります。

---

品質管理ソフトは、下記をクリックして下さい。
本館：エクセル将棋館（品質管理ソフト）